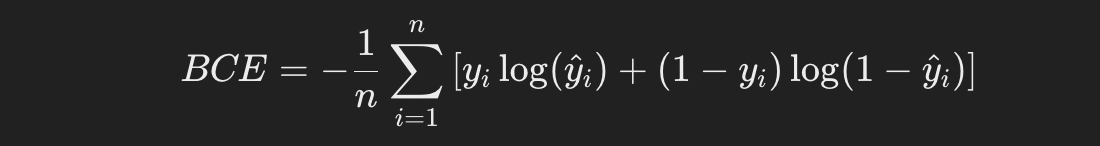반응형
손실함수(Loss Function)는 머신러닝과 딥러닝 모델에서 모델의 예측값과 실제값 간의 차이를 수치적으로 표현한 함수입니다. 모델이 얼마나 잘못 예측했는지를 나타내며, 이 값을 최소화하는 것이 학습의 목표입니다.
주요 손실함수 유형
*회귀 문제
평균제곱오차(Mean Squared Error, MSE)
: 실제값(yi)과 예측값(y^i)의 차이를 제곱하여 평균을 구함. 차이가 클수록 더 큰 패널티를 줌.
평균절대오차(Mean Absolute Error, MAE)
: 차이의 절댓값 평균을 구함. 이상치(outlier)에 덜 민감.
*분류 문제
이진교차엔트로피(Binary Cross-Entropy)
: 예측확률(y^i)이 실제 클래스(yi)에 가까울수록 손실이 작아짐.
다중교차엔트로피(Categorical Cross-Entropy)
: 여러 클래스 간 확률 분포를 비교하며, 정답 클래스 확률을 높이는 방향으로 학습.
*특수 목적
허브 손실(Huber Loss)
: MSE와 MAE의 장점을 결합하여 이상치에 덜 민감한 회귀 문제용 손실함수.
KL 발산(Kullback-Leibler Divergence)
: 확률 분포 간의 차이를 측정.
특징
손실함수가 모델의 학습 방향을 결정합니다.
선택한 손실함수에 따라 모델의 성능이 크게 달라질 수 있습니다.
각 문제(회귀, 분류 등)에 적합한 손실함수를 선택해야 합니다.
파이썬 구현 예제
*평균제곱오차 (Mean Squared Error, MSE) 구현 예제
평균제곱오차는 예측값과 실제값의 차이를 제곱하여 평균을 구합니다.
import numpy as np
def mean_squared_error(y_true, y_pred):
return np.mean((y_true - y_pred) ** 2)
# 예제
y_true = np.array([3, -0.5, 2, 7])
y_pred = np.array([2.5, 0.0, 2, 8])
mse = mean_squared_error(y_true, y_pred)
print("MSE:", mse)*평균절대오차 (Mean Absolute Error, MAE) 구현 예제
평균절대오차는 예측값과 실제값의 차이의 절댓값을 평균합니다.
def mean_absolute_error(y_true, y_pred):
return np.mean(np.abs(y_true - y_pred))
# 예제
mae = mean_absolute_error(y_true, y_pred)
print("MAE:", mae)
*이진 교차 엔트로피 (Binary Cross-Entropy) 구현 예제
이진 교차 엔트로피는 이진 분류 문제에서 주로 사용하는 손실함수입니다. 모델의 예측값이 확률값(0~1)이어야 합니다.
def binary_cross_entropy(y_true, y_pred):
epsilon = 1e-15 # 로그 계산 시 무한대로 발산하지 않게 하기 위해 작은 값 추가
y_pred = np.clip(y_pred, epsilon, 1 - epsilon)
return -np.mean(y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred))
# 예제
y_true = np.array([1, 0, 1, 1])
y_pred = np.array([0.9, 0.1, 0.8, 0.6])
bce = binary_cross_entropy(y_true, y_pred)
print("Binary Cross-Entropy:", bce)
*다중 교차 엔트로피 (Categorical Cross-Entropy) 구현 예제
다중 교차 엔트로피는 여러 클래스 중 하나를 예측할 때 사용하는 손실함수입니다.
def categorical_cross_entropy(y_true, y_pred):
epsilon = 1e-15
y_pred = np.clip(y_pred, epsilon, 1 - epsilon)
return -np.sum(y_true * np.log(y_pred)) / y_true.shape[0]
# 예제
y_true = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]])
y_pred = np.array([[0.7, 0.2, 0.1], [0.1, 0.8, 0.1], [0.2, 0.2, 0.6]])
cce = categorical_cross_entropy(y_true, y_pred)
print("Categorical Cross-Entropy:", cce)
*허브 손실 (Huber Loss) 구현 예제
허브 손실은 이상치에 민감하지 않은 회귀 손실 함수로, 평균제곱오차와 평균절대오차의 절충안입니다.
def huber_loss(y_true, y_pred, delta=1.0):
error = y_true - y_pred
is_small_error = np.abs(error) <= delta
squared_loss = 0.5 * (error ** 2)
linear_loss = delta * (np.abs(error) - 0.5 * delta)
return np.mean(np.where(is_small_error, squared_loss, linear_loss))
# 예제
huber = huber_loss(y_true, y_pred)
print("Huber Loss:", huber)
정리
손실함수는 "모델이 얼마나 실수했는지"를 숫자로 나타내는 잣대입니다. 숫자가 작아질수록 모델이 예측을 더 잘하고 있다는 뜻입니다.
반응형
'AI > 관련 자료' 카테고리의 다른 글
| [머신러닝] 배치 하강 경사법(Batch Gradient Descent) 정리 (0) | 2024.11.20 |
|---|---|
| [머신러닝] 활성 함수(Activation function)란? (0) | 2024.11.15 |
| [딥러닝] 원-핫 인코딩이란? / One-hot (0) | 2024.11.14 |
| [딥러닝] 텐서플로 케라스란? / TensorFlow Keras (0) | 2024.11.14 |
| [머신러닝] 차원 축소와 주성분 분석 (0) | 2024.11.11 |