시그모이드 활성 함수는 S-자 형태의 곡선을 가지며, 입력값을 0과 1사이의 값으로 매핑합니다.
시그모이드 함수는 아래와 같은 수식으로 정의됩니다.

여기서:
x는 입력값 (뉴런의 가중합), e는 자연상수 ()입니다.
특징:
- 출력 범위: 항상 0에서 1 사이의 값.
- 비선형성: 입력값이 클수록 출력은 에 가까워지고, 작을수록 에 가까워짐.
- 미분 가능: 역전파(Backpropagation)에서 사용할 수 있는 미분 값을 제공.
은닉층에서의 역할
시그모이드 함수는 은닉층에서 비선형성을 추가하는 데 사용됩니다. 이는 뉴런이 단순히 선형 연산만 하는 것이 아니라 복잡한 패턴을 학습할 수 있도록 도와줍니다.
주요 역할:
- 패턴 학습: 선형으로 분리되지 않는 데이터의 복잡한 패턴을 모델이 학습 가능하게 만듦.
- 정규화 효과: 값이 0과 1 사이로 제한되므로 극단적인 값의 영향을 줄임.
한계:
- 기울기 소멸 문제(Vanishing Gradient Problem): 입력값이 또는 로 갈수록 함수의 기울기(미분 값)가 매우 작아져 학습 속도가 느려질 수 있음.
출력층에서의 역할
시그모이드 함수는 출력층에서 이진 분류 문제를 해결하는 데 자주 사용됩니다. 출력값이 0과 1 사이로 제한되므로 확률로 해석할 수 있습니다.
예: 이진 분류 문제
- 이메일이 스팸인지 아닌지(스팸일 확률: 0~1).
- 환자가 질병에 걸렸을 확률을 예측.
출력값을 특정 임계값(예: 0.5)과 비교하여 스팸 여부를 결정하거나 질병 여부를 판별합니다.
실제 사례와 예시
1. 이진 분류 문제: 이메일 스팸 필터
- 입력 데이터: 이메일의 길이, 특정 단어 빈도수 등.
- 출력값:
0.8: 이메일이 스팸일 확률 80%.
0.2: 이메일이 스팸일 확률 20%.
출력값이 0.5 이상이면 스팸으로 분류.
2. 로지스틱 회귀: 고객 이탈 예측
- 입력 데이터: 고객의 소비 패턴, 연령, 과거 구매 기록.
- 출력값:
고객이 서비스를 떠날 확률(예: 0.7: 이탈 가능성 70%).
시그모이드 함수의 그래프와 직관적 이해
일 때: σ(0)=0.5 (중간값)
x→∞ : σ(x)→1
x→−∞ : σ(x)→0
그래프 직관
- 입력값이 작을수록 출력은 0에 가까움.
- 입력값이 커질수록 출력은 1에 가까움.
- 중간 영역에서는 입력값 변화에 따라 출력값이 민감하게 변동.
정리
은닉층: 복잡한 패턴 학습.
출력층: 확률로 해석 가능한 이진 분류 문제 해결.
활용 사례: 이메일 스팸 필터, 고객 이탈 예측, 의료 진단 등.
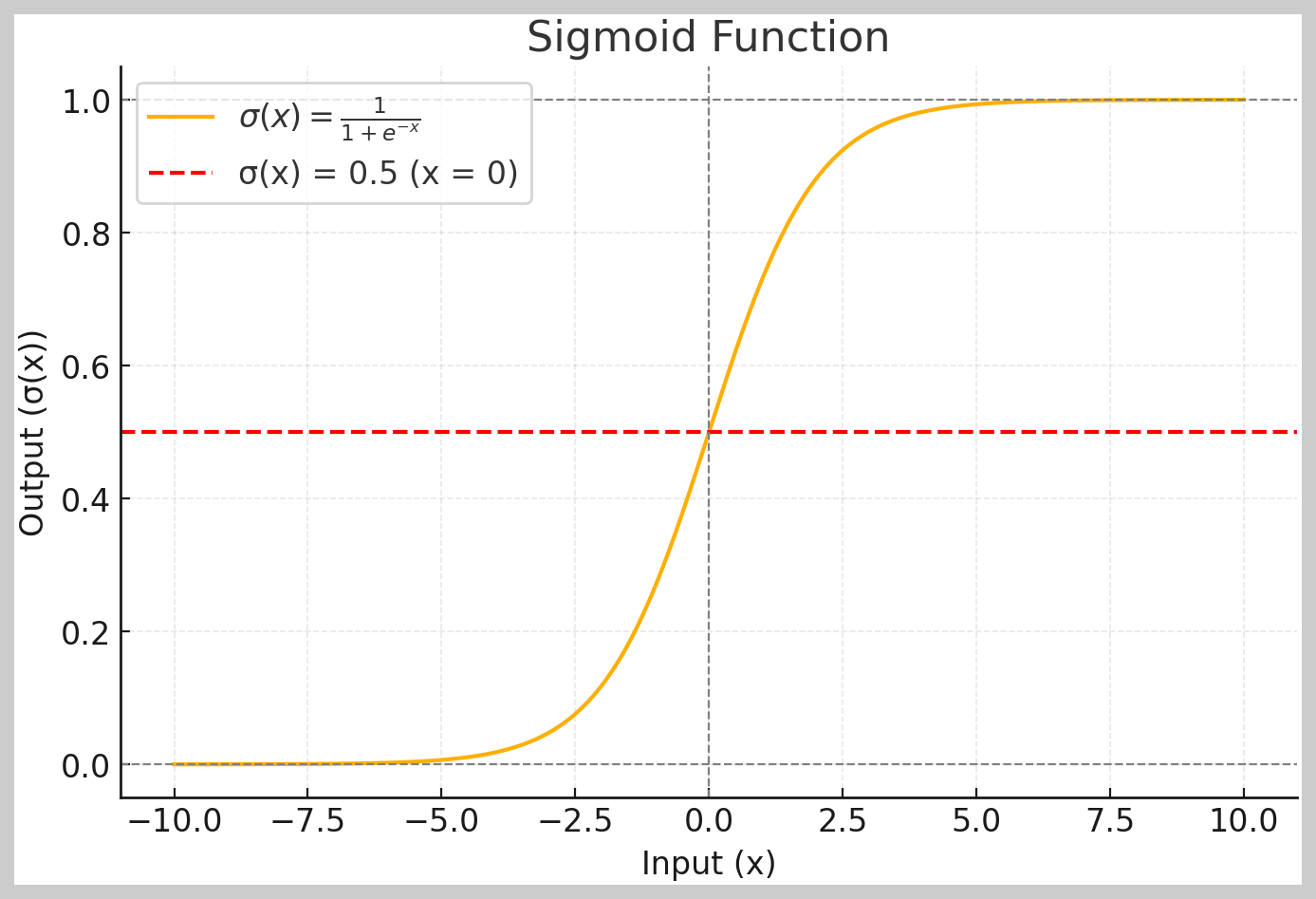
위 그래프는 시그모이드 함수의 모습을 보여줍니다.
- x값이 에서 까지 변할 때, 출력 값이 과 사이로 변화하는 것을 볼 수 있습니다.
일 때 출력은 정확히 0.5입니다(빨간 점선).
- x→∞일 때 출력은 1에 가까워지고, x→−∞일 때 출력은 0에 가까워집니다.
'AI > 관련 자료' 카테고리의 다른 글
| [머신러닝] 렐루(ReLU) 함수란? (2) | 2024.11.22 |
|---|---|
| [머신러닝] 미니 배치 경사 하강법(Mini-Batch Gradient Descent) 정리 (0) | 2024.11.21 |
| [머신러닝] 배치 하강 경사법(Batch Gradient Descent) 정리 (0) | 2024.11.20 |
| [머신러닝] 활성 함수(Activation function)란? (0) | 2024.11.15 |
| [머신러닝] 손실 함수(Loss Function)란? (0) | 2024.11.15 |



